“Work = force × distance” is a standard principle of physics which also occurs in all standard calculus textbooks in the form of the integral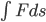 
. Unfortunately, standard textbooks never tell you why work is force times distance. Stewart's Calculus, for instance, has an entire section on “Work” in the chapter on “Applications of Integration.” Dozens of exercises are stacked up where we are asked to compute the “work” involved in this or that physical scenario. We are expected to dutifully plug numbers into formulas and get other numbers out like obedient robots, but why? What is the point of all these numbers? Why would anyone want to calculate the “work” so defined, and what does it really tell us? No justification is given. This is simply “the definition” of work, and one cannot “prove a definition,” so the reasoning seems to go. So the mere fact that some quantity is defined is taken as sufficient motivation for computing it in a bunch of instances. Presumably, the student is left to infer, this technical sense of the word “work” is supposed to have some sort of relation to the everyday sense of the word, which also seems vaguely applicable in the examples, as they usually involve mechanically moving stuff around. However, why it should be “force times distance” instead of, say, “force times time” or “force squared times distance” or whatever is not made clear. Also, the unit of “work” comes out as Joules, it is noted, which elsewhere in the book is taken as a unit of energy. So apparently “work” is related to (or is?) energy? But this mysterious connection is not explained. As we see, the student will be left with more questions than answers as soon as she tries to go even a little beneath the surface. The message is clear: this is no place for thinking; this book is about plugging numbers into formulas like a circus monkey doing tricks for a banana.
In intellectual mathematics we do not put up with this kind of nonsense. If we are going to talk about “work” we are not going to introduce it by authoritarian decree (“that’s the equation, now go plug numbers into it!”). Instead we are going to show you how you yourself can arrive at the notion of work by a natural line of reasoning using your own physical intuition and understanding. The below is an excerpt from my calculus textbook showing how this can be done.
An object of mass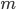 
at a not-too-great height 
above the surface of the earth has a potential energy of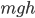 
. This means that we could, potentially, have it do so much work for us. You can think of for example a water wheel driven by a water fall: this device takes advantage of the potential energy stored in the water by virtue of its altitude, and harnesses it for some other purpose. Thinking in terms of water wheels, it is easy to understand why potential energy is proportional to mass and height. For if the height is double, you can have the water run through twice as many wheels on its way down, so you get twice as much work out of it. And if the mass is double you can split it in half and run each part through the water wheels separately, which makes it clear that you get twice the work in this case also. By the same argument we obtain the general relation work = force × distance which may be taken as the formal definition of work, as above.
Potential energy is energy by virtue of position; kinetic energy is energy by virtue of velocity. Water can drive a water wheel not only by falling from a certain height (potential energy) but also by rushing ahead in a stream at a certain velocity (kinetic energy). I shall now prove to you that just as potential energy is measured by 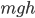, so kinetic energy is measured by 
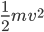. First I want make it clear that kinetic energy is “stored work.” Imagine yourself pushing a wagon along a railway track. When you are done pushing and let the wagon go, all the work you put into it is now “stored” in the wagon in the form of kinetic energy. We can get it back out again for example by our prototype method of water wheels, which we could have the wagon set spinning as it hits them along its path. Experience shows that it takes the same amount of effort to stop the wagon as it did to get it moving, so it is clear that the amount of work stored in the wagon is the same as that you put into it.
When you push the wagon to get it moving you are applying a certain force across a certain distance. The product of the two is the work you do, we saw above. This, then, is a measure of the kinetic energy, but not a very nice one. Kinetic energy is quite clearly intrinsic to the moving wagon, so it is awkward to characterise it in terms of the action of the worker who set it moving and however long of a run-up he used. We should much prefer to express it in terms of the mass and velocity of the wagon. But this is easily done, for we know that force = mass × acceleration, distance = average velocity × time. “Distance” here means the length of your run-up before you released the wagon, and “time” how long you took to complete it. Let’s say that you push equally hard throughout, so that the force, and thus acceleration, is constant.
Exercise. Conclude from this that the kinetic energy is .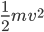
The two forms of energy that we have studied are clearly interchangeable: when an object falls it “trades in” potential energy for kinetic, and conversely when its velocity is directed upwards. By means of some ramps we could turn a water fall into a stream and conversely, so we would quite like to know which is better for driving water wheels. But it turns out to be all the same. The economy of nature is such that the exchange rate in these kinds of transactions is one to one. Energy is conserved. This agrees with experience but we can also prove it formally.
Exercise. Prove, by taking its time-derivative, that the total energy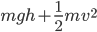 
is constant for a freely falling object.
Another useful way of establishing this sort of result is to prove that if it didn’t hold one could exploit the discrepancy to build a perpetual-motion machine which could create energy out of nothing, which is known to be impossible or at least a point on which we would be very pleasantly surprised to be proven wrong.
Exercise. Argue on such grounds that 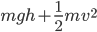is constant.