In a recent paper I argued against the standard view that Copernicus was influenced by late medieval Islamic astronomers. Below are some additional points on this paper that have come up in discussion.
Stanford Encyclopedia of Philosophy. I am happy that my paper is now cited in the Copernicus article of the Stanford Encyclopedia of Philosophy. However, the characterisation there of my paper is not the one I would use. It says: “Blåsjö claimed there was enough difference between Copernicus’s planetary models and those of the late Islamic astronomers that Copernicus could have derived them directly from ancient models.” But in my view it is not a question of “enough difference.” There is indeed some difference, contrary to the rhetoric of some who call the models “identical,” but by and large my point is rather that the very notion that degree of similarity implies influence is foolish in the first place. Scientists trying to solve the exact same problems with the exact same tools within the exact same tradition are bound to produce virtually identical solutions, regardless of whether they have ever heard of each other or not. So even if there was no difference at all it would still be realistic to imagine that Copernicus based his work on ancient theories only.
Hand verification of Mercury argument refutation. In my paper I showed that the Mercury argument that has for 40 years been considered “perhaps the best evidence” was based on a mathematical error and is simply factually incorrect. In the paper I gave a complex-exponential formula for the orbit of Mercury on the basis of which everything can be computed. At least one reader, however, has wished to confirm the matter for himself with hand calculations. Very good, to do this you may proceed as follows. Consider the value I give as 48.81º in my paper. Get Swerdlow’s translation of the Commentariolus and consult figure 39. Let the Earth be in Mercury’s line of apsis, and Mercury itself at 66.2º to this line. So in the notation of the figure we have 
= 180º and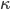 
= 66.2º. Introduce a coordinate system by 
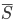=(0,0) and O=(25,0). Then 
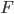= (9.4 cos 66.2º, 9.4 sin 66.2º) and 
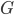= (9.4 cos 66.2º + 1.683, 9.4 sin 66.2º) and 
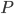= (9.4 cos 66.2º + 1.683 + 0.567, 9.4 sin 66.2º) = (6.043, 8.601). The angle 
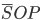is then arctan(8.601/(25-6.043)) = 24.40º. We have the same angle on the other side when 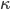= –66.2º, so the total visual size of the orbit must be at least 2*24.40º = 48.8º. Thus Mercury appears to move on a much smaller orbit than this (namely 46.5º), just as Copernicus says.
Tusi couple versus epicycle. One perceptive reader suggested the following counterpoint to my argument. I discuss Copernicus’s models for Mercury and the Moon. In both models I note that the last step was to introduce a radius correction. In the Mercury model this is done by a Tusi couple and in the Moon model by a simple extra epicycle. But since the functions of these two radius-correction components are so similar, why use one device in one case and another in the other? It seems like an arbitrary choice, and the fact that Copernicus and Ibn al-Shatir make the same choice therefore suggests influence after all.
To this I reply: The Tusi couple and Moon epicycle are indeed very similar in function and could almost be used interchangeably. But not quite. For the Moon one could use a Tusi couple instead of the extra epicycle, but this would mean using more circles than necessary. Since a single epicycle is enough this is preferable, and that is why it is used by both Copernicus and Ibn al-Shatir. But for Mercury one cannot use an epicycle in place of the Tusi couple. In Copernicus’ model the Tusi couple is at the base of the main epicycle. If it was replaced by an epicycle it would change not only the radius but also it would also move the main epicycle backwards and forwards in its orbit. For the Moon there is no such problem since the epicycle is outermost, so that only its motion along the orbit matters; it also has motion in the radial direction (towards and away from the earth) but this effect is very small and does not cause any problems. In the Mercury model the Tusi couple is not outermost, so if it was replaced by an epicycle both it’s motions would have a noticeable effect, even though only one of the effects is wanted. One needs the Tusi couple (i.e. morion purely in the radial direction) in order not to have such repercussion effects that ruin the rest of the model.