Don’t teach things that don’t serve a purpose. Or to put it differently: Pick up a calculus textbook and open an arbitrary section. Look at the problems at the end of the section and ask yourself: Is there any reason to want to know the answer to these problems? Are the problems inherently interesting, and the substance of the section a means to answering them? Then this is a meaningful topic and it should be taught. Or are the problems artificially concocted for the sole purpose of testing you on the material just introduced? Then it’s a crap topic and should not be taught. Students have no reason to work on such problems except subservience to the instructor, and therefore their effect is to suppress independent thought.
If we grant this as an axiom of teaching, it follows that traditional Calculus I courses must be reformed as follows.
Cut limits. Limits are a hotbed of pseudo-problems that do not serve any meaningful purpose. Monstrous fractions involving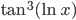 
, double substitutions, triple l’Hôpital’s rule problems and god knows what else: these problems are fake, fake, fake. They are not taught because they are genuinely needed to address genuinely interesting questions. They are made up for the sake of making up drill problems. They create unreflective and slavishly rule-following students, because any student who thinks for himself will immediately come to the conclusion that the class is a meaningless drill with no purpose.
Cut proto-“real analysis.” To the above it will be objected that limits caters to thinking students in that it addresses why the calculus works. So it is alleged, but it is not true. First of all the mass of drill problems assigned have absolutely nothing to do with such why-questions, so this false motivation is a dishonest bait-and-switch. Furthermore the why-questions at hand can be understood perfectly well without the pretentious machinery of limits. This is proved by history, where all leading mathematicians for over a hundred years understood the calculus perfectly without ever bothering with limits.
If you are serious about addressing why-questions you start with why-questions and develop the theory needed to answer them. It then soon becomes apparent that a few basic and intuitive notions are enough to deal with the matter to everyone’s satisfaction, which is indeed precisely what happened historically.
The charade continues with supposedly “conceptual” questions about a barrage of artificially contrived, piecewise defined functions pock-marked with a plethora of discontinuities and medley of different types of non-differentiability. A strange form of unconscious communism seems to be at the bottom of this approach: if “all functions are equal” then indeed it makes sense to give these fake examples as much screen time as the sine and the logarithm. But anyone who starts with interesting and meaningful questions, instead of making up problems to fit their preconceptions of what they have to teach, it is evident enough that some functions are more interesting than others, and that wasting half a calculus course nitpicking about exceptional qualities of the most artificial ones is a pointless exercise in pedantry.
To pretend that these kinds of things are needed to understand “the foundations” of basic calculus is a lie. I suspect most students realise as much, in their guts if not fully consciously.
Limit theory, exceptional functions, and real analysis rose together in the 19th century, more than a hundred years after the calculus had already flourished and produced everything a calculus student has any reason to be interested in. To be sure, all these things served a meaningful purpose then. The 19th-century conception of the foundations of the calculus is profound and important and served to resolve important enigmas that had arisen in the meantime. Of course I do not belittle or deny the value of such investigations in any way––on the contrary I would love to teach them in a real analysis class––but I also observe that they have nothing to do with basic calculus.
Real analysis is a wonderful subject, and calculus is a wonderful subject, but they are two completely different subjects. Don’t try to mix them in some Frankensteinian fashion, and most of all don’t lie to your students and pretend that analysis is the thinking student’s calculus. In reality it is the opposite: only the gullible, subservient student buys this bogus myth.
Include differential equations. The usual battery of integration techniques are usually accompanied by “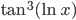”-style problems, much like the limit sections attacked above. Should they therefore be committed to the flames also? Not at all. The situation could not be more different, although students (and perhaps not a few teachers) in a traditional calculus course wouldn’t know it. Unlike the nonsense real analysis material artificially shoehorned into Calculus I, integration techniques do serve a very credible purpose that is very easily made evident to students. It only takes one simple reshuffling of the order of the topics: teach differential equations as early as possible, as I do in my book. This simple recipe at once changes the entire nature of drill problems on integration techniques. Without differential equations the students will conclude, with good justification, that these problems are nothing but a cruel obstacle course with no purpose. But with differential equations the student cannot draw the same conclusion without denying the value of studying population dynamics, the motion of rockets and projectiles and planets, and a thousand other fascinating and useful things besides. Hence we must either teach differential equations in Calculus I, or accept widespread hatred of mathematics as a rational outcome of our own doing.