I came up with this taxonomy when trying to explain certain conflicts and research choices that shaped the early history of the calculus. Below are a number of episodes that fit these categories very well. (For more details on the earlier systems, see this useful essay.)
Maestro philosophy: “Few but ripe.” It is a mark of class to focus only on elegant, simple, important, emblematic masterpieces. Write enough to give a definitive, impeccable treatment of the subject, but not more. It will be evident that this is merely the tip of an iceberg, resting on a solid body of technical expertise. But the tedious explication of the latter—the scaffolding, the tricks of the trade—is left to lesser Technocrat mathematicians.
E.g. Archimedes:
17th century Maestro examples:
Huygens: tautochrone = cycloid = evolute of cycloid.
Leibniz:
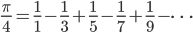
Non-examples:
Johann Bernoulli:
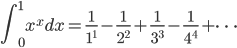
Not Maestro because not classically motivated and self-contained; presupposes “nerd” Technocrat interest in evaluating everything that can be symbolically formulated. Same with Euler’s so-called beautiful (actually only Technocrat) formula
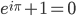
A typical Maestro versus Technocrat conflict/misunderstanding: Leibniz versus the English on power series in the 1670s.
Leibniz typical Maestro, cares about singular, beautiful results: “I possess certain analytical methods, extremely general and far-reaching,” but “exquisite”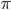 
series “especially is most wonderful.”
English typical Technocrat, care about plug-and-chug-ready formulas, criticise Leibniz for merely giving special cases. Collins: “infinite Series to be generally fitted to any equation proposed, so that an Algebraist being furnished with his Stock, will quickly fitt a Series.” Newton: I gave “a general Method of doing in all Figures,” whereas “Leibnitz never produced any other Series than numerical Series deduced from them in particular Cases.”
But Leibniz has no interest in Technocrat that doesn’t lead to Maestro: “I too used this method [of series inversion] at one time, but after nothing elegant had resulted in the example which I had by chance taken up, I neglected it forthwith with my usual impatience.”
Later Newton turns from Technocrat to Maestro, because more classical and elegant (and perhaps associated with a certain snobbery and sense of superiority): “He thought Huygens’s stile and manner the most elegant of any mathematical writer of modern times, and the most just imitator of the antients. Of their taste, and form of demonstration, Sir Isaac always professed himself a great admirer: I have heard him even censure himself for not following them yet more closely than he did; and speak with regret of his mistake at the beginning of his mathematical studies, in applying himself to the work of Des Cartes and other algebraic writers.”
Euler disapproves, goes back to Technocrat, values toolbox adaptability more than beauty: “I always have the same trouble, when I might chance to glance through Newton’s Principia: Whenever the solutions of problems seem to be sufficiently well understood by me, yet by making only a small change, I might not be able to solve the new problem using this method.”
Leibniz is by nature a Visionary. The Maestro tendencies in the 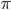series episode are coloured by the influence of Huygens, who, in typical Maestro manner, praised the 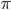series as “a discovery always to be remembered among mathematicians.”
Later Leibniz resisted Maestro and saw it as a distraction from his main task of Visionary. This is why, for example, he fights not to get drawn into the brachistochrone problem (a true Maestro problem): “The problem draws me reluctantly and resistingly to it by its beauty, like the apple did Eve. For it is a grave and harmful temptation to me.”
Visionary need Technocrat to spell out the details of their systems. E.g. Descartes: Van Schooten; Leibniz: l’Hôpital, Johann Bernoulli.
Leibniz: “I wish there were young people who would apply themselves to these calculations. With me it’s like the tiger who lets run whatever he does not catch in one or two or three attempts.”
Leibniz is no more than 5% Technocrat: “Had I 20 heads, or better yet 20 good friends, I would put one of them toward working out the theory of conics.”
Huygens: I will learn calculus but only for Maestro, not for Technocrat. “I still do not understand anything about ddx, and I would like to know if you have encountered any important problems where they should be used, so that this gives me desire to study them.” “[Natural] curves merit, in my opinion, that one selects them for study, but not those [curves] newly made up solely for using the geometrical calculus upon them.”
Leibniz: Agree, Technocrat calculus worth little. “You are right, Sir, to not approve if one amuses oneself researching curves invented for pleasure.” But the difference between Visionary and Maestro is that Visionary is more focussed on general methodological insights, which is why Leibniz adds: “I would however add a restriction: Except if it can serve to perfect the art of discovery.”
L’Hôpital’s Rule: typical Technocrat result of the sort condemned here.
Systematic theory of integration by partial fractions: a Technocrat topic needed for Visionary, namely “a question of the greatest importance: whether all rational quadratures can be reduced to the quadrature of the hyperbola and the circle” (Leibniz). This forces Leibniz, reluctantly and contrary to his nature, to do some Technocrat work, with poor results (Leibniz erroneously believes that “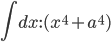
can be reduced to neither the circle nor the hyperbola by [partial fractions], but establishes a new kind of its own”). A typical Visionary, Leibniz clearly has very little interest in actually evaluating integrals, and only cares about giving a big-picture methodological-foundational account of integration in general.
Myth: Early Leibnizian calculus driven by applications; lacks attention to rigour. Hence typically Pragmatist.
Reality: The exact opposite: Early Leibnizian calculus primarily Visionary. It was actually indifferent to applications and was consumed by rigour, only rigour meant something completely different at that time. This is one of the main points of my book.