Podcast: Download
There is nothing counterintuitive about an infinite shape with finite volume, contrary to the common propaganda version of the calculus trope known as Torricelli’s trumpet. Nor was this result seen as counterintuitive at the time of its discovery in the 17th century, contrary to many commonplace historical narratives.
Transcript
Torricelli’s trumpet is not counterintuitive. Your calculus textbook lied to you.
You’ve probably heard of this cliché, Torricelli’s trumpet: an allegedly “paradoxical” shape that has infinite area but finite volume. It’s staple example in calculus textbooks. Well, there’s nothing to it, in my opinion. It’s a propaganda lie. Let’s revisionist-history the heck out this thing.
I will tell you why there’s nothing counterintuitive about this result. Then I’ll argue that it was not seen as counterintuitive at the time, in the 17th century, contrary to what everyone tells you. Then I will explain, in terms of the sociology of the mathematical community, why this myth is still so popular. That is to say, why it is such a comforting myth to so many people, despite being wrong.
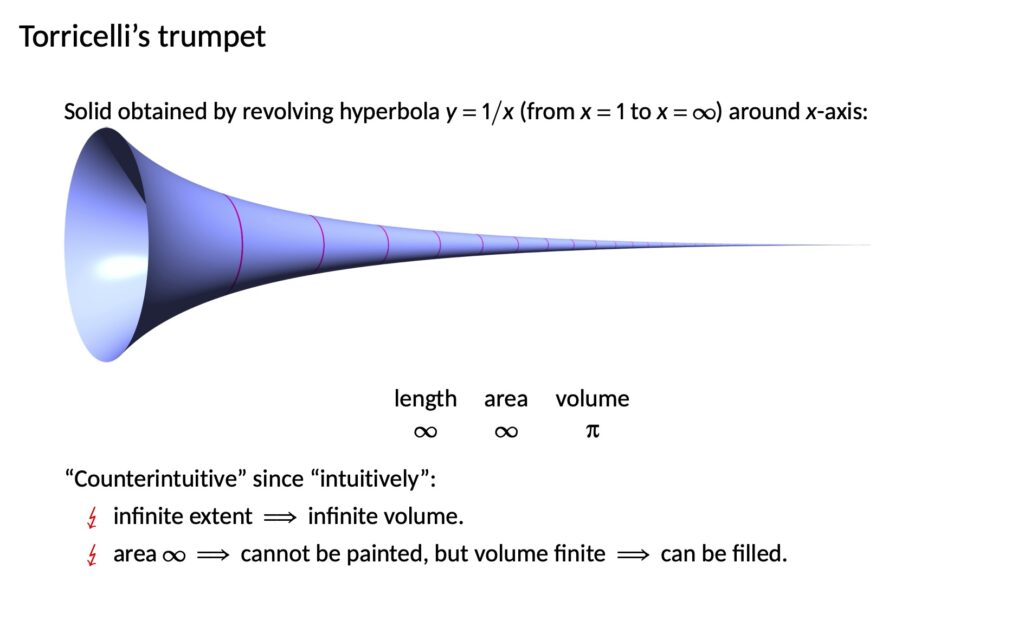
So, the trumpet. You take the hyperbola y=1/x and you rotate it about the x-axis. It makes a trumpet shape, a kind of funnel that becomes infinitely narrow the further you go.
Also known as “Gabriel’s Horn.” Actually I tried to look up the origin of this silly name but I couldn’t find it. I guess it was perhaps coined for the American market? “Torricelli” is bit too “Euro” isn’t it? Now, “Gabriel’s Horn” on the other hand, there you have a nice pious biblical name.
Anyway, whatever you want to call it. The volume of the funnel is finite. For example from x=1 onwards. Despite its area and its length being infinite.
There are two supposed contradictions here. On the one hand, finite volume with infinite extent (infinite length) could be regarded as two contradictory properties that it would be surprising to find in the same solid, allegedly. Alternatively, finite volume with infinite area could also be seen as a clash of two incompatible properties: a shape having those two properties at the same time is supposed to be contrary to “intuition,” allegedly. Sometimes it is put like this: Such a solid cannot be painted, since it has infinite area, yet it can be filled with paint, since it has finite volume. But I think this can be a misleading move that mixes the issue of Torricelli’s trumpet with general issues of how infinite processes correspond to everyday experience, which is perhaps a separate source of so-called “counterintuitive” phenomena. The fact is that if Torricelli’s trumpet is supposed to be a surprising result, then the source of the contradiction is supposed to be the properties of volume, area, and length of this shape, and not some secondary intuitions about infinite processes in general.
In my opinion, the properties of Torricelli’s trumpet are not “counterintuitive.”

First, is it counterintuitive for a finite amount of paint to cover an infinite surface? Of course not. Let’s put it like this. Suppose you have a can of paint. Obviously it contains a finite volume of paint, such as one liter. Now, open the can and pour the paint on the floor. Think of a big floor, like a basketball court. Get a spatula and start spreading the paint across as much area as you can.
Where do you think this process will stop? This is mathematical paint. You can spread it as thin as you like. How much area can you cover, if you can spread the paint thinner and thinner and thinner?
What does your “intuition” tell you? Does your “intuition” say that this spreading process with terminate after a certain number of square meters of the floor painted? Of course not. That would be idiotic.
And yet that is precisely what the standard account of Torricelli’s trumpet would have you believe. It is supposed to be “counterintuitive”, the story goes, for a finite volume of paint to cover an infinite area. Well, we have just seen that that premise is idiotic. Obviously a finite amount of paint can spread further and further, as long as you make it thinner and thinner. There is nothing “counterintuitive” about that.
Why would “intuition” say that the process of spreading the paint thinner and thinner would suddenly terminate at some finite bound? Why on earth would it? What would be the “intuitive” reason for why you could spread paint thinner, and then thinner, and then thinner, and then thinner, and then not thinner all of a sudden? Where would this invisible upper bound come from? Why would “intuition” stipulate the existence of such a ghost? It makes no sense.
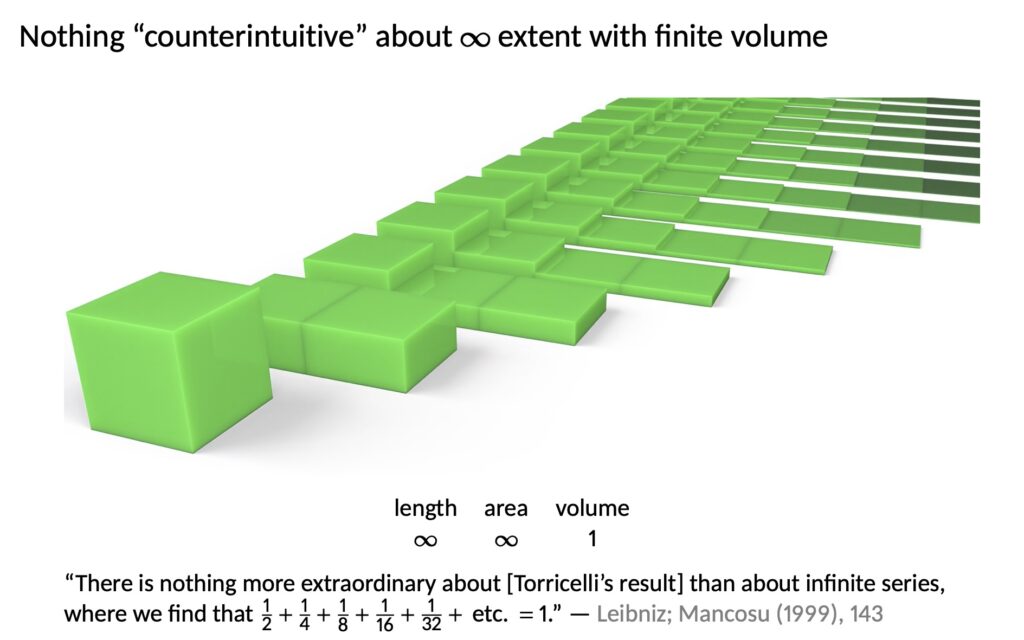
Here’s another thought experiment that proves the same thing. We’re not using paint anymore, but rather a cube. You have a cube of unit volume in front of you. You cut it in half, horizontally. Like a sandwich. Then you place the top half side-by-side with the bottom half. Next cut the top half in half again in the same manner, and bring the new top slice down next to the bottom slice. So now you have a kind of stairway with three steps.
Continue in the same way: you keep bisecting the last piece and placing all the pieces in a row. All the slices have a length and a width of 1, the original dimensions of the cube, because you are always cutting horizontally. You are cutting the heights in half, leaving the width and the breadth of all the pieces the same throughout.
So you get a row of blocks that each have a length and width of 1, and whose heights are 1/2, 1/4, 1/8, 1/16, and so on. The total volume remains 1 throughout the process of course, because you only moved the existing volume around without adding to it or taking anything away. Meanwhile, both the length and the area of the combined shape clearly approaches infinity, as is intuitively clear.
So with this simple intuitive argument we get infinite extent with finite volume. So clearly infinite extent with finite volume is by no means contrary to intuition.
Note that this simple thought experiment also shows that Torricelli’s trumpet is not a case of a technical mathematical result being philosophically or qualitatively different from simple common-sense examples, contrary to what calculus teachers like to pretend. So the standard story is wrong in two ways. It claims that advanced calculus proves intuition wrong. But that’s doubly a lie. First, intuition is not wrong, and furthermore you don’t need fancy calculus to show any of this anyway. The simple thought experiments of the repeatedly bisected cube or the painted basketball court, which you can explain to a 5-year-old, contain everything that is relevant. There is nothing qualitatively new added by the use of calculus.
These things were also well understood historically. For example, Isaac “Barrow … clearly saw that [Torricelli’s] theorem can be intuitively explained by the fact that ‘the infinite diminution of one dimension compensates the infinite increase of the other’.” This fits with the basketball court example. Although Barrow was talking about the relationship between volume and length, not volume and area. But the point is the same.
The equivalent of the bisected cube example was also well understood. For example, Leibniz rightly remarked that “there is nothing more extraordinary about [Torricelli’s result] than about infinite series, where we find that 1/2 + 1/4 + 1/8 + 1/16 + 1/32 etc. = 1.” Exactly. Nothing to see here. Just as Leibniz says.
Let’s turn to history then. Let’s see what people thought back then, besides Barrow and Leibniz. Torricelli published his result in 1641. In fact, all this stuff about area plays no part in the 17th century. The whole thing is about volume only. Torricelli’s trumpet has finite volume and infinite extent, that is to say, infinite length. That’s it. No area, no paint, no painting an infinite area. Nobody said anything about that in the 17th century. Just volume and length.
Still, even then many people today say that this was a big paradox back then. Lots of mainstream accounts of the history of mathematics repeat this story. For example, here is a quote from Simmons’s book Calculus Gems: “That a solid can have finite volume even though it has infinite extent … caused great astonishment at the time.” Another example, from Burton’s History of Mathematics: “The result seemed so counterintuitive and astonishing that at first some of the leading European mathematicians thought it impossible.” And here’s another example, from the book When Least Is Best by Nahin: “Prior to this discovery it was commonly accepted that a surface extended to infinity would necessarily have to be of infinite size, that is, enclose infinite volume.”
So, that’s what everybody says. But here at this podcast we are not in the business of repeating boring clichés like some people, so let’s have a go at it. All of these people are wrong, in my opinion.
I’m going to base my discussion on Paolo Mancosu’s book Philosophy of Mathematics and Mathematical Practice in the Seventeenth Century. This is by far the most complete and authoritative historical account of all of this, of the reception of Torricelli’s trumpet in the 17th century. Mancosu covers the relevant historical sources quite exhaustively. I am going to use the same sources, but I am going to interpret them differently.

Mancosu himself is of the same opinion as all these other guys I quoted, team cliché. According to Mancosu, I quote him, Torricelli’s result “seemed so counterintuitive and astonishing that, at first, some of the leading mathematicians thought it impossible.” “There are good intuitive grounds for holding that an infinitely long solid cannot have a finite volume,” and that is what gave rise to “the intuitive, widespread, and erroneous inference from infinite length to infinite volume.”
So Mancosu is wrong like everybody else, in my view. Let’s look at his evidence and refute it all one by one.

First, Mancosu’s chapter on this stuff is off to an interesting start. He says: “Even eighty years later Bernard de Fontenelle commented: ‘One apparently expected, and should have expected, to find [Torricelli’s solid] infinite [in volume].’”
Ha! Did you catch that rhetorical trick? “Even eighty years later …” “Even”! In fact, instead of “even eighty years later” it would be more accurate to say: not until eighty years later is this allegedly common view actually explicitly asserted, and then by an essayist and not a mathematician. It’s neither here nor there what some non-mathematician wrote 80 years later. He could very well have been subject to the same biases as the modern proponents of the story.

So, let’s look further back in time. What were Torricelli’s own words? Indeed, Torricelli called his result “as it were paradoxical,” in Mancosu’s translation. The Latin is “ut ita dicam paradoxicum.” I think maybe a more literal translation would be “so to speak paradoxical.” “So to speak”: that is to say, not actually.
It’s not a paradox but it’s kind of like a paradox if you squint a bit, Torricelli seems to be saying. Of course that seems to give some credence to the standard interpretation, perhaps the strongest evidence that exists for this view. Fair enough. There is some connection to paradox, like the standard story says. On the other hand, Torricelli’s phrasing is also a notably guarded formulation coming from the discoverer himself. You would think that Torricelli, the very discoverer of this result, would be inclined to play up, if anything, the philosophical significance of his own theorem. Despite this incentive, Torricelli evidently felt the need for the qualifier “so to speak paradoxical.” The result is not actually paradoxical, in other words.
Torricelli then goes on to explain why the result is “so to speak” paradoxical: “The reason is that ‘if one proposes to consider a solid … infinitely extended, everybody immediately thinks that such a figure must be of infinite size’.” Again, this fits to some extent with the standard narrative. But on the other hand it is striking how much more restrained this wording is. The Latin for “immediately” is “statim,” which arguably means something like “the very instant that,” or in other words: before thinking about it for more than a few seconds. Quite plausibly, Torricelli has chosen his words carefully since he is well aware of examples such as that of the repeatedly bisected cube that I described before. Perhaps Torricelli knows well that if he asked a mathematician colleague whether a solid with infinite length must necessarily have infinite volume then they would likely very soon think of such counterexamples and realise that the answer is no. Perhaps that is why Torricelli does not say that his theorem contradicts what everybody believes, or that it contradicts intuition. Instead he merely says, much more cautiously, that his result is “so to speak” surprising since it is different from the first example of a solid with infinite length that pops into someone’s head the very split second that they are asked to imagine such a shape.
Quick! Think of a shape with infinite length! Ok, maybe then you think of a shape that also has infinite volume. But that is not the same as to say that “intuition” says that it must have infinite volume.
Let’s listen to Torricelli’s words again: “if one proposes to consider a solid infinitely extended, everybody immediately thinks that such a figure must be of infinite size.” That is to say, in that moment, when you are asked to picture such a shape, your “immediate” impulse is to think of one that has infinite size. That’s your “immediate” reaction. Not your considered reaction, not your mathematician’s intuition, not what you think after a bit of thought. Only “immediately.” Torricelli has chosen his words wisely, so that it seems like he is saying a lot but in fact he is carefully choosing a formulation that is not subject to refutation based on thought experiments like the ones I gave before, because Torricelli is only talking about “immediate”, split-second visualisation, and he wisely says nothing about what somebody who thought about it for two minutes would think. In this way Torricelli stops well short of asserting the standard view that I quoted from so many modern historians. Torricelli seems to be going in that direction but he doesn’t go anywhere near as far as those statements from the modern literature that I quoted.
That’s all we have to go on in terms of Torricelli’s own words. Now let’s turn to the reaction of Torricelli’s contemporaries.

It is true, as the standard story says, that a number of mathematicians at the time reacted with some surprise to Torricelli’s result. But here we must ask ourselves: Why were they surprised? The standard story assumes that they were surprised because the result was counterintuitive. Therefore contemporary expressions of surprise are often cited as self-evidently supporting the standard story. But in fact there are other good reasons for contemporary mathematicians to have been surprised that have nothing to do with intuitions about infinite shapes.

Torricelli’s work showed that infinite curvilinear figures are mathematically tractable. That in itself was novel and surprising, quite apart from the specific result and whether it was intuitive or not. Indeed, Torricelli explicitly makes this point himself: “Among all the solids of which ancient and modern authors have determined the measures with much effort, none, as far as I know, has an infinite extension.”
Exactly. It was rare indeed for geometers at this time to be able to go qualitatively beyond what the ancient masters such as Archimedes had done, as opposed to supplementing and extending their results with more of the same. In fact, the very nature of the ancient methods for determining areas and volumes, which was still the gold standard in Torricelli’s time, and which he still relied on for proving his result in the most rigorous way, would seem to preclude application to infinite figures, as Torricelli himself noted: “In introducing the proof by exhaustion, Torricelli remarked that it would seem an impossible task to inscribe in another figure a figure of infinite length, or to circumscribe another figure around such a figure.”
In fact, therefore, when we have historical evidence that certain 17th-century mathematicians found Torricelli’s result to be “impossible,” we cannot infer that they therefore regarded the volume result as counterintuitive. Instead, the impossibility in question could be what Torricelli himself called the seemingly “impossible task” of applying rigorous exhaustion methods to infinite figures. And that is a methodological matter entirely independent of the specific content of Torricelli’s theorem and its intuitiveness or lack thereof.
There are indeed some historical testimonies that are ambiguous in this respect. For example, according to Torricelli himself, “Roberval considered this proposition false and impossible; actually, when Father Mersenne came by here he told me that Roberval, having thought about it for some time wrote I don’t know what demonstrations or speeches in order to prove that my proposition was absurd and impossible.” This is as consistent with the standard intuition-centred narrative as with the alternative intuition-independent narrative that I have proposed. Maybe Roberval thought the result was impossible because of his intuition about infinite shapes, or because he though it was not methodologically possible to apply rigorous geometry to such shapes. After all, why had Archimedes not done it, if it could be done?
Other 17th-sources are inconclusive in the same way. For example, Cavalieri said about Torricelli’s result that it is “extraordinary that that could be.” Again a generic expression of surprise. That is not enough to establish a link to any intuition or common conviction that solids of infinite extent ought to have infinite volume. Indeed, Cavalieri wrote to Torricelli that “I do not know how you fished out its measure so easily in the infinite depth of that solid.” So here Cavalieri is clearly highlighting that it is the new reach of the mathematical methods that is surprising rather than the result itself.

There is another sense too in which Torricelli’s result could have been seen as surprising in a way that has nothing to do with geometrical intuitions about infinite volumes. Namely, that the theorem invokes the notion of an actual infinity. Classically, statements involving infinity were often studiously avoided in favour of equivalent finitistic formulations. For example, instead of “there are infinitely many primes,” Euclid says “prime numbers are more than any assigned multitude of prime numbers” (Elements IX.20). But no such finitistic paraphrase was forthcoming in the case of Torricelli’s theorem. As Mancosu says, “The notion of actually infinite length is present in the very statement of the theorem. Moreover, the proofs themselves, as they stand, make sense only if the hyperbolic solid is given as infinitely long in actu.” But “Torricelli’s result is boldly infinitistic,” and efforts by purists “at reducing it to a finitistic framework appear destined to fail.”
One such finitism purist was Hobbes. In his view, as summarised by Mancosu, “any consideration of infinity, both geometrical and arithmetical, ought to be banished. Hobbes claimed that when mathematicians use the word ‘infinite’, what they usually mean, or ought to mean, is ‘indefinite’, that is, as great, or small, as one pleases.” “In Hobbes’ mathematical universe …, to talk about a solid ‘whose sides are extended out to infinity is absurd’.”

This is certainly a crucial background to keep in mind when interpreting Hobbes’s comments on Torricelli’s result. Hobbes claimed that “to understand [Torricelli’s theorem] for sense, it is not required that a man should be a geometrician or a logician, but that he should be mad.”
This striking quote is often connected with the intuition narrative. For example, The Cambridge Companion to Hobbes says: No, it is not necessary to be mad to accept Torricelli’s result. “Rather, of course, it is required that one should see, as Hobbes sometimes failed to do, that mathematics can raise and resolve problems where physical experience is lacking and physical intuition may deceive.” That’s the opinion of The Cambridge Companion to Hobbes, which is in line with the standard view.
But note indeed that Hobbes is not claiming that the theorem is contrary to “physical intuition.” Instead he says that it has no “sense.” This is in line with the standard finitistic position in philosophy that statements involving infinity have meaning (or “sense”) only when they can be, and are, reformulated in finitistic terms.

But, this point aside, there is one final passage in Hobbes that Mancosu regards as an outright explicit affirmation of the standard intuition-centred interpretation, leading Mancosu to confidently assert that “Hobbes believed that natural light teaches us that an infinitely long solid, however subtle, must exceed in volume any finite solid.” “Natural light” is indeed a synonym for intuition, so, if substantiated, this would make a strong case for the standard narrative. The Hobbes passage in question is the following.
“It has been demonstrated, they say, by Torricelli that a certain acute hyperbolic solid, in this sense of infinite [namely, greater than any assignable measure], is equal to a [finite] cylinder. … The distance which Torricelli supposes infinite is to be understood as indefinite. Nor could it be understood differently by him, who in quite many demonstrations uses Cavalieri’s principle of indivisibles, which are such that their aggregate can be equated to whatsoever given magnitude. Therefore, a proposition as absurd as this that the infinite is equal to the finite, must not be attributed to Torricelli. In fact, as it is clear by the natural light, there cannot be a solid so subtle which does not infinitely exceed every finite solid.”
So those are Hobbes’s words, and according to Mancosu’s interpretation he is saying that Torricelli’s result is counterintuitive.
But if you parse the quote you see that there a number of problems with Mancosu’s reading of this passage. For one thing, note that Hobbes clearly connects his conclusion to Torricelli’s use of Cavalieri’s principle, that is to say, his method of proof, by means of infinitesimals or indivisibles. But if Hobbes is trying to say that the result itself is counterintuitive, then why does it matter what method was used to prove it? Hobbes is saying that something is contrary to “natural light,” which means contrary to intuition, but what exactly? The passage is not so clear, but apparently the point is connected to the method of proof, and not merely to the content of the theorem itself.
Indeed, the crucial final sentence of Hobbes’s passage is difficult to parse altogether. It appears to be nonsensical on the face of it. The thing that is evident by “natural light” or intuition according to Hobbes is that: “there cannot be a solid so subtle which does not infinitely exceed every finite solid.”
This sounds crazy. It appears to say that any “subtle” (that is to say, small) solid must be infinite, which is obviously nonsense. I checked Hobbes’s original Latin but unfortunately that’s just as ambiguous and it doesn’t clarify anything.
For Mancosu’s reading to work, it seems that this crucial sentence, about any “subtle” body being infinite, must be interpreted as follows.
The passage starts:
“There cannot be a solid…”
Here, for Mancosu’s reading, we should think of Torricelli’s trumpet as the solid in question.
“There cannot be a solid so subtle…”
“Subtle” here then means thinning out or tapering off, as the trumpet does when it goes to infinity.
“There cannot be a solid so subtle which does not infinitely exceed every finite solid.”
So, first of all, for this not to be nonsense we must, for Mancosu’s reading to work, we must insert an extra clause that must be regarded as implicit in Hobbes:
Instead of: “There cannot be a solid so subtle which does not infinitely exceed every finite solid.”
We must read: “There cannot be a solid [that is infinitely extended and yet is] so subtle which does not infinitely exceed every finite solid.”
If we twist the passage like this then indeed it does say that the volume of Torricelli’s trumpet must exceed any finite volume. That is to say, it must be infinite. That is how Mancosu wants to read it.
I don’t agree. I will propose a different interpretation. But first let’s summarise the problems with Mancosu’s interpretation. First there is the connection to the method of proof, that is to say to the use of infinitesimal slices. Hobbes says: Torricelli used Cavalieri’s method and “therefore” etc. Hobbes’s conclusion is a consequence of the method of proof used. Which is not reflected in Mancosu’s interpretation of the concluding sentence. Mancosu’s interpretation only has to do with the statement of the theorem and not with its proof.
Furthermore, for Mancosu’s reading to work we had to insert that the solid Hobbes was talking about had to be infinite in extent even though Hobbes doesn’t say that. We would have to regard that as implied by context. Which is certainly questionable.
And one more thing: I don’t know if you caught this but Hobbes used the phrase “infinitely exceed every finite solid.” In Mancosu’s reading he’s saying: Any infinitely extended solid, no matter how thin it gets or how much it tapers off, will “infinitely exceed every finite solid.”
Why “infinitely”? That’s completely redundant isn’t it? You could just as well have just said: it exceeds every finite solid. If you exceed every finite solid you are infinite already. Of course if you only finitely exceed some finite solid then you are obviously yourself finite. So of course you cannot then exceed every finite solid. So if you exceed every finite solid, then you also automatically exceed every finite solid by infinitely much, so to speak. Because if you exceeded one of them only by a finite amount then you couldn’t also exceed all the other ones.
So Mancosu’s reading doesn’t explain why Hobbes uses this redundant word “infinitely” which doesn’t add anything and doesn’t change the meaning in any way. This word could have been omitted and the sentence would have meant exactly the same thing, according to Mancosu’s interpretation. Although Mancosu himself doesn’t mention that, of course.
Now I am going to propose my alternative reading, which avoids all of these problems.
Hobbes’s sentence starts:
“There cannot be a solid…”
Here I claim that we should not in fact think of Torricelli’s trumpet. Instead, the solids Hobbes is thinking of here are the infinitesimal components dV, the Cavalieri slices, of the trumpet volume. In other words, the slices that are used to calculate the volume, basically calculus-style. These dV’s, these infinitesimal components of volume, are what Hobbes is speaking about, I claim.
Let’s continue reading Hobbes’s sentence:
“There cannot be a solid so subtle…”
That is to say, so small: dV = epsilon. We are doing a finitistic paraphrase of a calculus argument. A limit-style paraphrase. Where the volume element dV is some very small real number epsilon.
Back to Hobbes:
“There cannot be a solid so subtle which does not infinitely exceed every finite solid.”
There cannot be any epsilon that is so small that it does not, when taken infinitely, that is to say added to itself any number of times, does not eventually exceed any given real number. This is the Archimedean property of the real numbers, in other words.
This is why we need the word “infinitely” that didn’t serve a purpose in Mancosu’s interpretation. The little number epsilon, the dV, is, taken singly, just a very small thing of course, but taken “infinitely” (that is to say added together over and over and over again) it eventually becomes greater than anything.
This reading explains why the link with the Cavalierian method of proof is crucial to the point, just as Hobbes seemed to indicate. It also explains why the phrase “infinitely exceed,” as opposed to merely “exceed,” is needed. It also does not require a crucial phrase that dramatically impacts the meaning to be postulated as implicit.
According to my reading, Hobbes’s statement is in effect simply an assertion of the Archimedean property of the real numbers, which was a well-known axiom that many greater mathematicians than Hobbes did not hesitate to regard as evident by “natural light.” Therefore Hobbes’s claim, on this reading, is correct and unproblematic, and does not have anything to do with physical or geometrical intuitions about infinite volumes.
Nor is Hobbes’s point an impactful critique of Torricelli’s reasoning for that matter, since Torricelli does not rely on non-Archimedean assumptions in the manner Hobbes seems to be trying to suggest. But that is beside the point for our purposes.

This concludes my analysis of the historical reception of Torricelli’s theorem. I think there is very little evidence to say that it was regarded as counterintuitive at the time, contrary to the standard narrative in the literature. What I have discussed is essentially all the evidence. I have systematically gone through basically all passages from 17th-century sources that are commonly cited in support of the standard narrative. There’s nothing more. There is no smoking gun anywhere. There are only these passages, all of which can be interpreted very differently than in the standard story, as I have shown.
Now I will add a little speculation about why I think the myth of Torricelli’s trumpet is so popular. Basically, I believe this is ultimately because the way we teach calculus is poorly motivated.
Modern calculus textbooks are monstrosities. They mix classical calculus with modern real analysis as if they were one and the same subject, which they are not.
One moment you are doing applications of integration by parts, and the next moment you are thinking about whether continuity implies differentiability.
These are both great subjects. I love calculus: going nuts with integration by parts, applying it to a bunch of differential equations and physics and stuff. Wonderful.
And I love real analysis. Such an elegant, unified theory that brings such razor clarity to so many tricky questions. “Baby Rudin” is a work of art. It is stylistic perfection.
But these are two separate subjects. Modern calculus textbooks don't want you to know this. Modern calculus textbooks pretend that real-analysis-style rigor is the correct and appropriate lens through which to understand classical calculus. Which it is not.
Mathematicians who teach calculus pretty much know this in their heart of hearts, even if they try to repress it. They know that the need for real-analysis-style rigour in calculus serves no reasonable purpose in that course. They know that you could do the entire calculus course completely unrigorously and it would be perfectly fine.
Unlike real analysis, of course. You couldn’t teach that course intuitively or informally. Doing it formally is precisely part of the core of what makes the subject great. Formal rigour in real analysis is very well motivated. It is a beautiful course for that reason.
But formal rigour in calculus is largely pointless and serves pretty much no purpose within calculus itself. The so-called rigorous approach to calculus didn’t exist for the first 200 years of calculus, when all the best applications of calculus were worked out by all the best mathematicians of the day who were the most accomplished calculus practitioners the world has ever seen, perhaps more so than anyone alive today because there are no research professors of calculus anymore.
Mathematicians who teach calculus know all of this. The know that the calculus has always thrived without rigour. They know that every single one of the great applications of calculus were developed with complete disregard for real-analysis-style rigor. At some level they know this, at least subconsciously. They may try to suppress this knowledge because it makes their life easier.
They have to teach real-analysis-style proofs in calculus courses, so it would be easier for them if doing so was a good idea. Otherwise they are torturing students with lots of difficult technicalities that are poorly motivated.
You can see now why Torricelli’s trumpet is a godsend to these people. Supposedly, Torricelli’s trumpet shows that intuition cannot be trusted. In other words, it motivates taking much more formal and rigorous approach to calculus.
Phew! As an instructor you had seen your students suffering from the overly formal approach, and you had felt bad about it. Maybe in a moment of weakness you had even wondered to yourself why indeed we have to teach calculus this way, although you would certainly keep those kinds of speculations to yourself.
It is a weight on your conscience as a calculus instructor. Am I just torturing my students with vastly excessive technicalities for no good reason?
What you need to be able to sleep well at night is a nice self-rationalising story that tells you that you are doing the right thing. “Ah, well, you see, this rigour may be a bitter medicine for some but you need it! It’s for the best! It’s for your own good!”
And how do we prove that rigour in calculus is actually a good thing? Oh well, a good example is Torricelli’s trumpet, you see.
These people desperately need the standard story of Torricelli’s trumpet to be true. It is exactly the self-rationalising justification they need to keep teaching the way they do and convince themselves that their conscience is clear. It is a necessary myth.
That is why so many people do not want to know the real history of Torricelli’s trumpet. They would rather have the comforting myth that flatters the status quo.
