Let us define the support that the hypothesis  receives from the evidence
receives from the evidence  as the increase in its probability:
as the increase in its probability: 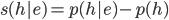 . Popper & Miller [1987, p. 574] prove that this support function may be split into two terms:
. Popper & Miller [1987, p. 574] prove that this support function may be split into two terms:
\begin{equation}\label{one}s(h|e)=s(h\lor e|e)+s(h\leftarrow e | e).\end{equation}
It is easy to evaluate these terms, which shows that the first term is always positive (or 0):
\begin{equation}\label{dedsup} s(h\lor e|e)= 1-p(h \lor e),\end{equation}
while the second term is always negative (or 0):
\begin{equation}\label{indneg} s(h\leftarrow e | e)=- \left ( 1-p(e) \right)\left ( 1-p(h|e) \right).\end{equation}
From here Gillies [1986, p. 111] is lured into concluding the refutation of induction as follows:
"Since 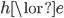 follows logically from
follows logically from  ,
, 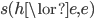 must represent purely deductive support. So, if there is such a thing as inductive support in the Bayesian sense, it must be contained in the term
must represent purely deductive support. So, if there is such a thing as inductive support in the Bayesian sense, it must be contained in the term 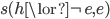 . However ... this term is always negative. It therefore follows that there cannot be inductive support of the kind that the Bayesians postulate."
. However ... this term is always negative. It therefore follows that there cannot be inductive support of the kind that the Bayesians postulate."
But to say that "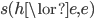 must represent purely deductive support" is naive. As Townsend [1989, pp. 493f.] points out, it is clear from (2) that such a stipulation has absurd consequences, namely that any hypothesis is deductively supported by any evidence (unless
must represent purely deductive support" is naive. As Townsend [1989, pp. 493f.] points out, it is clear from (2) that such a stipulation has absurd consequences, namely that any hypothesis is deductively supported by any evidence (unless 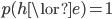 ). In particular, a contradictory hypothesis
). In particular, a contradictory hypothesis 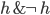 receives deductive support, as does a hypothesis which is directly contradicted by the evidence.
receives deductive support, as does a hypothesis which is directly contradicted by the evidence.
Popper and Miller are not as naive as Gillies. They never explicitly identify 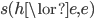 with deductive support. How, then, do they conclude their proof that there can be no inductive support? They are actually alluding to two different ways of completing the proof. Let me begin with the first of these, which is related to Gillies'. In fact, while this approach appears more sophisticated, I shall argue that it is still susceptible to the same criticism.
with deductive support. How, then, do they conclude their proof that there can be no inductive support? They are actually alluding to two different ways of completing the proof. Let me begin with the first of these, which is related to Gillies'. In fact, while this approach appears more sophisticated, I shall argue that it is still susceptible to the same criticism.
Note first that "unless  happens to be deductively independent from
happens to be deductively independent from  , the value of
, the value of 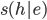 is deductively contaminated." (This and the following quotations are all from Popper & Miller [1987, p. 574]. They are insubstantially edited.) That is to say: if
is deductively contaminated." (This and the following quotations are all from Popper & Miller [1987, p. 574]. They are insubstantially edited.) That is to say: if  and
and  have common consequences, then
have common consequences, then  will be supported by having these consequences confirmed. But this is deduction, not induction: the evidence does not point beyond itself. But
will be supported by having these consequences confirmed. But this is deduction, not induction: the evidence does not point beyond itself. But 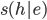 is presumably inductively contaminated as well. How are we to disentangle one contaminant from the other? Gillies' simplistic approach will not do, as we know. Nevertheless, one feels that
is presumably inductively contaminated as well. How are we to disentangle one contaminant from the other? Gillies' simplistic approach will not do, as we know. Nevertheless, one feels that 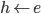 is the key. "If there is such a thing as pure inductive dependence at all, there seems nothing for it but to measure it by something like
is the key. "If there is such a thing as pure inductive dependence at all, there seems nothing for it but to measure it by something like 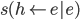 ," which is not deductively contaminated because nothing (nontautological) can be derived from both
," which is not deductively contaminated because nothing (nontautological) can be derived from both  and
and 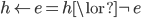 , so there can be no deductive support in this case. We already know that
, so there can be no deductive support in this case. We already know that 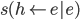 is negative by (\ref{indneg}), so it is tempting to jump to the conclusion that inductive support is negative. But this would be too hasty: how do we know that the inductive contamination of
is negative by (\ref{indneg}), so it is tempting to jump to the conclusion that inductive support is negative. But this would be too hasty: how do we know that the inductive contamination of 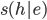 is negative simply because
is negative simply because 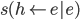 is negative? To solve this problem Popper and Miller make this very convenient assumption:
is negative? To solve this problem Popper and Miller make this very convenient assumption:
(A) "If there were to be some genuinely inductive dependence [i.e. inductive contribution to 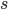 ] between a hypothesis
] between a hypothesis  and some evidence
and some evidence  , it could hardly change if
, it could hardly change if  were replaced by some hypothesis
were replaced by some hypothesis 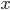 equivalent to
equivalent to  (given
(given  , or equivalent to
, or equivalent to  in the presence of
in the presence of  )."
)."
Indeed, 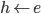 is equivalent to
is equivalent to  in the presence of
in the presence of  , so we have the desired result: "Inductive dependence is counterdependence," because it is so in the pure case
, so we have the desired result: "Inductive dependence is counterdependence," because it is so in the pure case 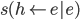 and thus also in all other cases by (A).
and thus also in all other cases by (A).
But isn't (A) just Gillies in disguise? Let us investigate the case where the evidence refutes the hypothesis, which was so embarrassing to Gillies. If we take 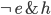 for our hypothesis we find that
for our hypothesis we find that 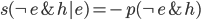 and
and 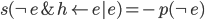 . Since in general
. Since in general 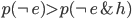 , this means that
, this means that 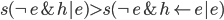 . According to (A) the inductive support should be the same in both cases, so apparently the difference must be due to some positive deductive support for
. According to (A) the inductive support should be the same in both cases, so apparently the difference must be due to some positive deductive support for 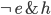 , which is absurd. This refutation of (A) is simpler than the only other refutation of (A) that I have found, namely that of Rodriguez [1987, pp. 356f.]. It seems so simple, indeed, that I cannot help but suspect that I am missing something in my interpretation of (A). But I can find no indication of this in Popper and Miller. They also follow the statement of (A) by saying "This much has recently been argued at length by Levi [1986]." This is an extremely leisurely piece without a single formula in it which indeed seems to embrace the simple interpretation of (A) that I have used (esp. p. 136).
, which is absurd. This refutation of (A) is simpler than the only other refutation of (A) that I have found, namely that of Rodriguez [1987, pp. 356f.]. It seems so simple, indeed, that I cannot help but suspect that I am missing something in my interpretation of (A). But I can find no indication of this in Popper and Miller. They also follow the statement of (A) by saying "This much has recently been argued at length by Levi [1986]." This is an extremely leisurely piece without a single formula in it which indeed seems to embrace the simple interpretation of (A) that I have used (esp. p. 136).
It seems that Popper and Miller were themselves aware of the dubious status of (A), for later they offered a second (more famous) proof which avoids it. The idea of this proof is:
(B) 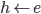 is the part of
is the part of  that goes beyond
that goes beyond  .
.
Here I am using the shorthand of identifying 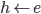 with its content, i.e., the set of all its (nontautological) logical consequences. From (B) Popper and Miller claim to prove their theorem roughly as follows: inductive support means support that goes beyond
with its content, i.e., the set of all its (nontautological) logical consequences. From (B) Popper and Miller claim to prove their theorem roughly as follows: inductive support means support that goes beyond  , but the part that goes beyond
, but the part that goes beyond  always has negative support by (3). QED.
always has negative support by (3). QED.
Popper and Miller justify (B) thus: "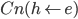 is just what needs to be added to
is just what needs to be added to 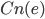 , without duplicating anything already there, in order to yield the system
, without duplicating anything already there, in order to yield the system 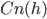 ." The problem is that in general most of
." The problem is that in general most of 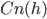 is in neither
is in neither 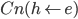 nor
nor 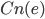 : such propositions can be derived only when the two are pooled. And yet such propositions clearly seem to go beyond
: such propositions can be derived only when the two are pooled. And yet such propositions clearly seem to go beyond  , so it seems that (B) patently fails to capture the part that goes beyond
, so it seems that (B) patently fails to capture the part that goes beyond  . Indeed, (B) "has been almost uniformly rejected" (Howson & Franklin [1994, p. 452]), primarily for this reason, and a number of convincing refutations of (B) using such propositions have been given. These examples span the range from simplistic logical ones (
. Indeed, (B) "has been almost uniformly rejected" (Howson & Franklin [1994, p. 452]), primarily for this reason, and a number of convincing refutations of (B) using such propositions have been given. These examples span the range from simplistic logical ones ( itself), to ravens, to actual scientific ones.
itself), to ravens, to actual scientific ones.
Such examples are summarised in Popper & Miller [1987, p. 580]. Their reply is revealing. They begin by admitting that "the facts are of course as stated." But then they insist that "the objection is devoid of merit" (p. 581). And why? Because "the objection misses its mark: it fails to show that positive probabilistic dependence can be achieved in the absence of some degree of deductive dependence"! Of course there can be no positive probabilistic dependence without some degree of deductive dependence. That is an immediate corollary of (1). Popper and Miller are trying to defuse a correct rebuttal of (B) by claiming that "its mark" was not (B) at all but rather a completely different theorem, and one with an elementary proof.
A second diversion they employ is to try to shift the burden of proof onto their critics by challenging them to characterise the excess content of  in a better way: "that, we feel, is a problem for those who believe in induction, not for us." (Miller [1990, p. 151]; cf. Popper & Miller [1987, p. 581]. This challenge has been taken up by Mura [1990] and Elby [1994].) Perhaps, but this does not change the fact that Popper and Miller's "proof" that deductive support is countersupport is only as good as their characterisation of excess content. One must conclude that they use these rather dishonest tricks because they have no convincing arguments in defence of (B). (Even their own disciple, Gillies [1986], apparently wished to avoid (B), which was his motivation for giving the foolish argument discussed above.)
in a better way: "that, we feel, is a problem for those who believe in induction, not for us." (Miller [1990, p. 151]; cf. Popper & Miller [1987, p. 581]. This challenge has been taken up by Mura [1990] and Elby [1994].) Perhaps, but this does not change the fact that Popper and Miller's "proof" that deductive support is countersupport is only as good as their characterisation of excess content. One must conclude that they use these rather dishonest tricks because they have no convincing arguments in defence of (B). (Even their own disciple, Gillies [1986], apparently wished to avoid (B), which was his motivation for giving the foolish argument discussed above.)
It may seem obvious that (B) is the weak point in the Popper-Miller argument, but actually quite a few attempted refutations mistakenly charge at other parts of it. I want to discuss the attempt of Good [1990]. Note first that it is not necessary to identify 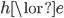 with the part of
with the part of  that does not go beyond
that does not go beyond  . To do so is a natural complement to (B), especially in light of (1), and Popper and Miller do indeed use this mode of expression. But as I outlined above one may prove that inductive support is countersupport from (B) alone. Thus it is not quite fair to formulate the Popper-Miller argument as if it depends crucially on this additional assumption, and then go on to reject it for this reason. And yet this is what Good [1990] does, for example. Here is what he calls a "suspicious feature" of the Popper-Miller argument:
. To do so is a natural complement to (B), especially in light of (1), and Popper and Miller do indeed use this mode of expression. But as I outlined above one may prove that inductive support is countersupport from (B) alone. Thus it is not quite fair to formulate the Popper-Miller argument as if it depends crucially on this additional assumption, and then go on to reject it for this reason. And yet this is what Good [1990] does, for example. Here is what he calls a "suspicious feature" of the Popper-Miller argument:
"Whatever  may be, whether it is supported or completely refuted by
may be, whether it is supported or completely refuted by  , or if it has nothing at all to do with
, or if it has nothing at all to do with  , it remains true that a 'part' of
, it remains true that a 'part' of  , namely
, namely 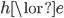 , is deducible from
, is deducible from  ."
."
Besides missing the core of Popper-Miller, this argument does not appear to me to be as "suspicious" as it first looks. If  and
and  are unrelated, then nothing nontrivial can be derived from both
are unrelated, then nothing nontrivial can be derived from both  and
and  separately, which means that nothing can be derived from
separately, which means that nothing can be derived from 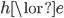 , which means that the content of
, which means that the content of 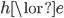 is in effect empty. Thus there is nothing suspicious about this case. And why is it suspicious that part of
is in effect empty. Thus there is nothing suspicious about this case. And why is it suspicious that part of  is deducible from
is deducible from  even when
even when  refutes
refutes  ? Take the simple case
? Take the simple case 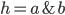 and
and 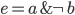 . The part of
. The part of  deducible from
deducible from  is of course
is of course 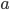 . In terms of content:
. In terms of content: 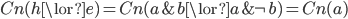 . Hardly very suspicious.
. Hardly very suspicious.
Good [1990] continues:
"[If  consists of these two parts,] Does this then put us under an obligation, whenever
consists of these two parts,] Does this then put us under an obligation, whenever  refutes
refutes  , to express this refutation by saying that
, to express this refutation by saying that  refutes
refutes 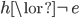 , thus removing from
, thus removing from  the part that
the part that  supports? I don't believe that Popper and Miller would use such an absurd mode of expression."
supports? I don't believe that Popper and Miller would use such an absurd mode of expression."
But this mode of expression is not absurd. It would in fact be perfectly sensible if (B) was correct. Consider an example: my hypothesis is Euclidean geometry 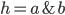 , where I have divided its assumptions into the parallel postulate
, where I have divided its assumptions into the parallel postulate 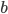 and the other axioms
and the other axioms 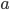 . Suppose the evidence tells us that space is non-Euclidean, that is:
. Suppose the evidence tells us that space is non-Euclidean, that is: 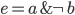 . Now
. Now  is refuted, but this does not mean that we should throw out all of
is refuted, but this does not mean that we should throw out all of 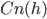 . On the contrary,
. On the contrary, 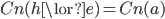 remains intact. To say that what is falsified is the part that goes beyond
remains intact. To say that what is falsified is the part that goes beyond  is to say that what is falsified is precisely the part of Euclidean geometry
is to say that what is falsified is precisely the part of Euclidean geometry 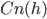 that can only be proved using the parallel postulate
that can only be proved using the parallel postulate 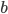 . The remaining part
. The remaining part 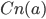 , which
, which  supports, includes the first handful propositions of Euclid's Elements. It should indeed be preserved. The problem for Popper-Miller is again (B): Pythagoras' theorem, for example, is a consequence of
supports, includes the first handful propositions of Euclid's Elements. It should indeed be preserved. The problem for Popper-Miller is again (B): Pythagoras' theorem, for example, is a consequence of  that clearly goes beyond
that clearly goes beyond  ; and yet it is obviously not in
; and yet it is obviously not in 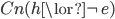 . Thus Good should have attacked (B) instead of this "mode of expression," which would in fact be correct if (B) was correct.
. Thus Good should have attacked (B) instead of this "mode of expression," which would in fact be correct if (B) was correct.
REFERENCES
Chihara, C. S. & Gillies, D. A. (1988). An Interchange on the Popper–Miller Argument. Philosophical Studies, 54, 1–8.
Elby, A. (1994). Contentious Contents: For Inductive Probability. The British Journal for the Philosophy of Science, 45(1), 193–200.
Gillies, D. (1986). In Defense of the Popper–Miller Argument. Philosophy of Science, 53(1), 110–113.
Good, I. J. (1987). A Reinstatement, in Response to Gillies, of Redhead’s Argument in Support of Induction. Philosophy of Science, 54(3), 470–472.
Good, I. J. (1990). Discussion: A Suspicious Feature of the Popper/Miller Argument. Philosophy of Science, 57, 535–536.
Howson, C. & Franklin, A. (1994). Bayesian Conditionalization and Probability Kinematics. The British Journal for the Philosophy of Science, 45(2), 451–466.
Levi, I. (1986). Probabilistic pettifoggery. Erkenntnis, 25(2), 133–140.
Miller, D. W. (1990). Reply to Zwirn & Zwirn. Cahiers du CREA, 14, 149–153.
Mura, A. (1990). When Probabilistic Support Is Inductive. Philosophy of Science, 57(2), 278–289.
Popper, K. R. & Miller, D. W. (1987). Why Probabilistic Support is Not Inductive. Philosophical Transactions of the Royal Society of London, A321, 569–596.
Rodriguez, A. R. (1987). On Popper–Miller’s proof of the impossibility of inductive probability. Erkenntnis, 27, 353–357.
Townsend, B. (1989). Partly Deductive Support in the Popper-Miller Argument. Philosophy of Science, 56(3), 490–496.