I am currently teaching an “introduction to proofs” course from a thoroughly run-of-the-mill textbook. Students need to learn to write proofs, sure enough, but in my opinion these kinds of courses are quite fundamentally misconceived in a number of respects.
First of all they assume that one can teach form without substance–––or in other words that it is a good idea to force students to slavishly follow the pedantic rituals of proof-writing without showing any of the actual mathematics that motivated the techniques in question. Thus we spend most of the course proving that if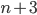 
is even then 
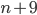is even and other extremely obvious and trivial results. The idea is to teach the craft of proof-writing without being distracted by difficult mathematics, but the reality is that we are forcing students to follow pedantic rituals without giving them any rational reason to do so. The obvious message is that mathematics is about pedantry for pedantry’s sake.
By teaching the ritualistic pedantry of proof-writing without content we are driving a wedge between normal, common-sense, intuitive reasoning and mathematical proofs. In this way we are crushing any inclination on the part of our students to think in a creative and independent way. We crush their attempts to try to grasp mathematics in a way that makes sense to them. We crush creativity and curiosity, and we impose unquestionable uniformity. By asking them to prove trivial things in a pedantic way we are telling them that their ways of reasoning are not mathematics, and that to become a mathematician they must transport themselves to a parallel universe where nothing that is natural or intuitive to them counts for anything, and where it is a capital offence to call an even number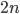 
without specifying that 
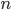is a whole number even though every normal person understand exactly what they mean.
Since we do not convey any credible purpose of what we teach, the students must accept the pedantic rules we insist upon even though they are completely unjustified. Making people follow arbitrary rules is a terrific way of crushing independent thought and instilling a crippling sense of fear in your subjects, as many dictators have been aware. Like an oppressed population fearing that the secret police will pounce upon them at any moment with arbitrary accusations, so our students are taught to live in fear of our pedantic mathematics. They soon learn to mimic the officially sanctioned examples and constantly ask the teacher’s permission before they attempt the slightest deviation: “Can you do that?” “Is that allowed?” But it is not careful analytical reasoning that makes them ask, it is fear of arbitrary rules and a complete alienation from any sense that they themselves can figure out what makes makes sense and what doesn’t.
We also learn to “prove” that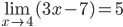 
using a ton of pretentious epsilonic machinery, without, of course, ever reaching anything remotely like a result for which such a machinery is appropriate. The technique of 
-proofs was developed in the 19th century to answer questions such as: Is the limit function of a convergent series of continuous functions continuous? Is every continuous function differentiable almost everywhere? Is every continuous function integrable? It is for these kinds of questions that an -approach makes sense. To use this technique instead (and only) to prove that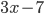 
is continuous at 
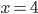is a parody of mathematics.
It is madness to imply to our students that such pompous proofs are somehow superior to common-sense, intuitive reasoning as far as the results we study are concerned. Using extremely pretentious language to say obvious things is the hallmark of the worst kind of drivel philosophy produced by poseurs in Paris. It’s a sad day when mathematicians of all people are beating these self-important faux-thikers at their own game.
Intro to Proof courses also have much in common with the idiotic “New Math” movement of the 60’s that everyone now agrees was disastrous. Just as “New Math” consisted in little more than expressing trivial ideas in pretentious Bourbaki-inspired terminology, so Intro to Proof courses fetishise the superficial trappings of mathematics without backing it up with any meaning or purpose. In fact, our book even has a whole bunch of “exercises” quibbling about the number of elements of 
and suchlike, exactly in the manner of “New Math” madness.
And did you know that, when proving a theorem of the form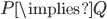 
, a proof is called “trivial” if it shows that 
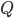is always true regardless of 
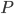, and “vacuous” if it shows that 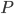is always false? Who on earth has ever used such ridiculous terminology for any credible purpose? It would be better to say that in either such case the theorem is called “stupid” and leave it at that. If 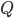is always true you would be better off just making that your theorem instead of giving a pointless name to 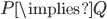, now wouldn’t you? But of course our textbook gives a hundred “exercises” on this ridiculous nonsense that has nothing to do with real mathematics, because it’s easier to teach stupid terminology than meaning and purpose.
Another problem with these kinds of books is that they select exercises the popular form of pseudo-learning in which students unthinkingly mimic an example template, changing only superficial details. Thus when studying induction we set out to prove a thousand pointless and artificially concocted arithmetic formulas. The only thing that is different from proof to proof is some basic algebra, which the students already know how to do, so by having them blindly go through the motions of writing proofs in this way one can create the illusion that learning is taking place, even though the exact opposite is achieved: the only part the students need to alter from proof to proof is the only part they didn’t need to practice, while the actual substance supposed to be taught (the structure of an induction proof) is the same from proof to proof and can therefore be ritualistically copied without thinking.
Another example of this is -proofs: we spend virtually all of our efforts doing algebra to find the specific expression for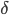 
needed to prove the (obvious) continuity of some specific function at some specific point. In other words, we completely miss the point of what -proofs are all about, and instead focus on exactly the one part that is the most insignificant, because that’s the approach that lends itself best to students mindlessly learning to go through the motions of drill exercises instead of actually doing any serious thinking.
Convergence or divergence of power series is done in the same mindless-algebra-crunching way. In fact, astonishingly, the book never even mentions why anyone would care whether a series is convergent or divergent, despite posing a hundred exercises on this exact topic. You do not “learn to write proofs” this way. What you learn is that meaning and purpose has no place in mathematics; that asking why anything is interesting or worth proving in the first place is a sure sign that you do not have a mathematical mind. This is the worst possible lesson you could teach young students, yet it is as if these kinds of books were determined to drive home this exact point.
By the time the course finally gets around to some actual substance toward the end, it has successfully eradicated any misconceptions in the students’ minds that mathematics might involve human communication and trying to figure things out using natural reasoning. Instead they will have learned that a mathematical proof is a sacred ritual and that no one is allowed into the sect of they do not learn to chant the spells in exactly the manner of the elders.
Consider for example this theorem and proof (the essential ingredient of the proof of the Schröder-Bernstein Theorem) from our textbook:
Someone who wanted to understand what is going on and feel why it’s true might put it instead like this:
Theorem. Let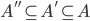 
and suppose there is a bijection 
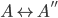. Then there is also a bijection 
.
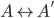Proof. Think of these sets as the populations of Sweden (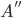
), Europe (
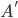), and the world (
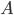). Imagine that all of these populations are infinite, and that every person lives alone in one apartment, and that every apartment in the world is occupied.
What does the bijection 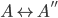mean in this context? It means everyone in the world can be matched up with a unique Swedish person. We might be tempted to think of it as “everyone marries a Swedish person.” But this would be misleading, because marriage is mutual: if I marry you, you marry me. But that is not what the bijection is saying. The bijection is not only pairing up non-Swedish with Swedish people. Swedish people are themselves part of the world population 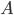, so they too get assigned another Swedish person in the course of the bijection. Therefore it is better to think of 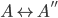as matching members of the world population with Swedish apartments. Since there was precisely one Swedish person per Swedish apartment to begin with this just another way of looking at the same bijection. This is a better analogy than marriage because it is not mutual: if I move into your apartment, you do not have to move into mine.
So the bijection says that the whole world can move into precisely one apartment each in Sweden. This will involve Swedish people moving around within Sweden to “make room” even though there was already one person per apartment (in the manner of “Hilbert’s Hotel”).
Given such a bijection, we want to find a bijection 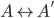. That is to say, we want a scheme for everyone in the world to move to Europe in such a way that every European apartment has precisely one person in it.
Maybe some natural disaster made much of the world uninhabitable, and the United Nations hired some mathematicians to figure out how to move everyone to Sweden, which they thought would be the only inhabitable country. But then it turned out the scale of the disaster was not as bad as thought, so actually all of Europe would still be inhabitable.
Therefore we are now facing the problem of how to adapt the original move-everyone-to-Sweden scheme and turn it into a move-everyone-to-Europe scheme. Intuitively we feel it must be doable since it should be “easier” than moving everyone to Sweden, but how exactly should we do it? We might be tempted to say: Everyone outside of Sweden but in Europe just stay put, and everyone in the rest of the world and Sweden move according to the original scheme. Sure enough this will get everyone to Europe. But it won’t fulfil the condition that no apartment be left empty. For in the original scheme Swedish people moved about to make room for other Europeans, and since those Europeans are now staying home these apartments will become empty.
Instead we must issue the following instructions. First everyone outside Europe move to the Swedish apartments assigned to them under the original scheme. This means a number of Swedish people will be “bumped” out of their apartments. Let them also move to the apartment assigned to them under the original scheme, and the same for those they bump out in turn, and so on. Let such repercussion moves play out in as many steps as needed, and let everyone not affected simply stay put where they are.
In this way we are left with precisely on person per apartment in Europe. For it is clear that no apartment is left empty since people only move after someone has taken their place. And it is clear that no two moving people are assigned the same apartment, since all moves take place according to the original moving scheme, which by assumption assigned everyone a unique apartment.
We have thus constructed a bijection between the world population and European apartments. By associating each European apartment with its original occupant (when there was precisely one European per European apartment before the moves), this gives a bijection between world population and Europeans, as required. QED.
This is the same proof in different words. It shows in plain and intuitive terms why the theorem holds. It also shows how to arrive at the solution, unlike the textbook proof, which pulls it out of a hat like magic. But God forbid, of course, that you should ever utter any reasoning of this form in a proofs course! That would be sacrilege of the first degree! No clearer proof could exist that you were not cut out to be a mathematician!
Is this the message we want to send our students? That it is more important to slavishly follow the sanctioned “house style” than to try to think and reason in an open-minded fashion that is convincing to yourself and to others? Or that using pretentious terminology and notation somehow makes an argument “more rigorous”?